二叉树中的最大路径和

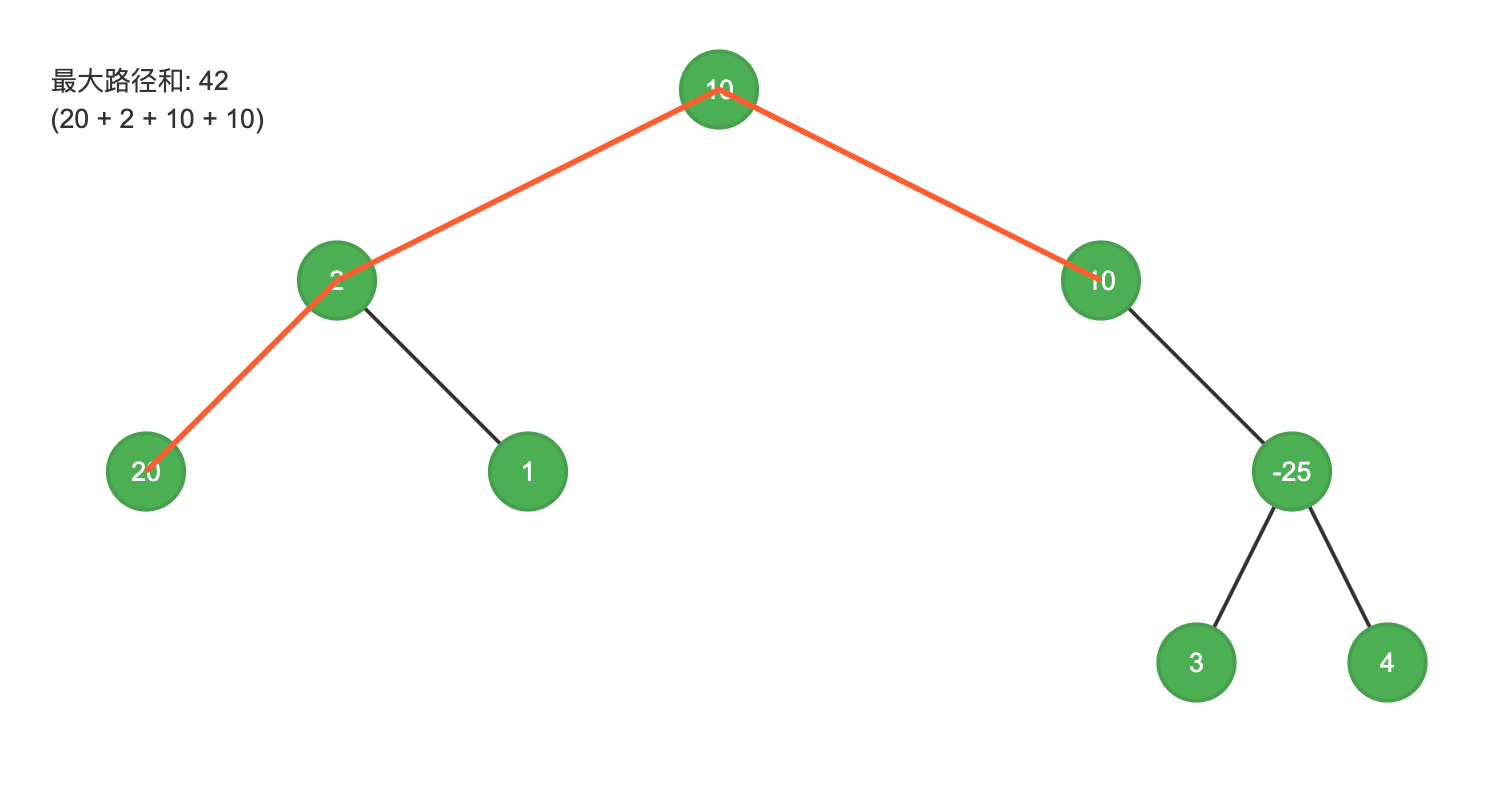
我们使用递归方法遍历树的每个节点。
对于每个节点，我们计算: a) 包含该节点和左子树的最大路径和 b) 包含该节点和右子树的最大路径和 c) 包含该节点及其左右子树的路径和
我们持续更新全局最大路径和（maxSum）。
函数返回当前节点能够贡献的最大值（节点值加上左子树或右子树中的较大者）。
这种方法的时间复杂度是O(N)，其中N是树中的节点数，因为我们需要访问每个节点一次。空间复杂度在最坏情况下（树完全不平衡）是O(N)，在最好情况下（树完全平衡）是O(log N)，这是由于递归调用栈的开销

package main

import (
	"fmt"
	"math"
)

// TreeNode 定义二叉树节点结构
type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

// 全局变量，用于存储最大路径和
var maxSum int

func maxPathSum(root *TreeNode) int {
	maxSum = math.MinInt32 // 初始化为最小整数
	maxGain(root)
	return maxSum
}

func maxGain(node *TreeNode) int {
	if node == nil {
		return 0
	}

	// 递归计算左右子树的最大贡献值
	leftGain := max(maxGain(node.Left), 0)
	rightGain := max(maxGain(node.Right), 0)

	// 当前节点的最大路径和
	priceNewPath := node.Val + leftGain + rightGain

	// 更新全局最大路径和
	maxSum = max(maxSum, priceNewPath)

	// 返回节点的最大贡献值
	return node.Val + max(leftGain, rightGain)
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func main() {
	// 构建示例二叉树
	root := &TreeNode{Val: 10}
	root.Left = &TreeNode{Val: 2}
	root.Right = &TreeNode{Val: 10}
	root.Left.Left = &TreeNode{Val: 20}
	root.Left.Right = &TreeNode{Val: 1}
	root.Right.Right = &TreeNode{Val: -25}
	root.Right.Right.Left = &TreeNode{Val: 3}
	root.Right.Right.Right = &TreeNode{Val: 4}

	fmt.Printf("二叉树的最大路径和为: %d\n", maxPathSum(root))
}

image.png|625